ABCDE (13023)
풀이코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
// 13023 ABCDE
const int MAX = 2000;
int n, m;
// 인접 행렬
bool arr[MAX][MAX] = {false};
// 인접 리스트 (2차원 배열)
vector<int> vec[MAX];
// 간선 리스트
vector<pair<int, int>> edges;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
for(int i = 0; i < m; i++){
int from, to;
cin >> from >> to;
// 인접 행렬
arr[from][to] = true;
arr[to][from] = true;
// 간선 리스트
edges.push_back({from, to});
edges.push_back({to, from});
// 인접 리스트
vec[from].push_back(to);
vec[to].push_back(from);
}
// 양방향 저장으로 m 2배
m *= 2;
for(int i = 0; i < m; i++){
for(int j = 0; j < m; j++){
// A -> B 로 가는 쌍 (간선 리스트 이용)
int A = edges[i].first;
int B = edges[i].second;
// C - > D 로 가는 쌍 (간선 리스트 이용)
int C = edges[j].first;
int D = edges[j].second;
// A, B, C, D 각각 다른지 체크
if (A == B || A == C || A == D || B == C || B == D || C == D) {
continue;
}
// B -> C 로 연결 되는지 확인 (한 정점에서 다른 정점으로 이어지는지 -> 인접 행렬 이용)
if(!arr[B][C]) continue;
// D에서 E 로 연결 되는 간선이 있는지 확인 (임의의 정점이 어떤 정점으로 이어지는지 -> 인접 리스트 이용)
for(int E : vec[D]){
if (A == E || B == E || C == E || D == E) {
continue;
}
cout << 1 << '\n';
return 0;
}
}
}
cout << 0 << '\n';
return 0;
}
재귀.. 시간초과
더보기
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
// 13023 ABCDE
const int MAX = 2000;
int n, m;
// 인접 행렬
// 간선에 가중치가 없기에 bool 형으로 그래프를 표현 가능
bool isFriend[MAX][MAX] = {false};
bool isVisted[MAX] = {false};
int max(int a, int b){
return a > b ? a : b;
}
int solve(int index){
// 기저 사례 : 모두 방문했으면 1 return
bool ok = true;
for(int i = 0; i < n; i++){
if(!isVisted[i]) ok = false;
}
if(ok) return 1;
int ret = 0;
for(int i = 0; i < n; i++){
// 이미 방문했으면 생략
if(isVisted[i]) continue;
// index 와 친구 관계라면
if(isFriend[index][i]){
isVisted[i] = true;
ret = max(ret, solve(i));
isVisted[i] = false;
}
}
return ret;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
for(int i = 0; i < m; i++){
int tmp1, tmp2;
cin >> tmp1 >> tmp2;
isFriend[tmp1][tmp2] = true;
isFriend[tmp2][tmp1] = true;
}
int ok = 0;
// 모든 점을 시작점으로 해봄.
for(int i = 0; i < n; i++){
fill_n(isVisted, MAX, false);
isVisted[i] = true;
if(solve(i)) ok = 1;
}
if(ok) {
cout << '1' << '\n';
}
else{
cout << '0' << '\n';
}
}해설
적용한 레시피 / 방법론 + 접근법
풀이
1-1. 인접 행렬
- 임의의 두 정점 사이의 간선이 있는지 확인 하는 것이 O (1) 이 걸림.
1-2. 인접 리스트
- 한 정점과 연결된 모든 간선을 찾는데 걸리는 시간이 O(차수) 이다.
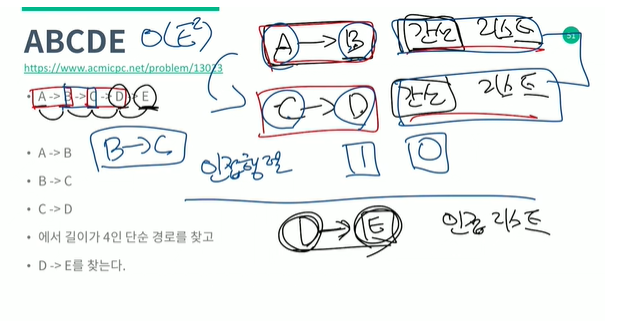
1-3. 간선 리스트
- 모든 간선을 저장해둔다.
2. 위 세가지의 그래프 저장방식을 모두 활용하여, 각 저장방식의 장점을 이용할 수 있을 때, 각각을 활용했다.
- 주석에 세세히 써둠.
아쉬웠던 부분 / 오답 원인 / 개선해야 할 점

반응형
'ps > bfs & dfs' 카테고리의 다른 글
| [bfs] 1697 숨바꼭질 (0) | 2021.10.02 |
|---|---|
| [dfs] [연결 요소] 단지번호붙이기 2667 (0) | 2021.10.02 |
| [dfs] 1707 이분 그래프 (0) | 2021.10.02 |
| 연결 요소의 개수 11724 (0) | 2021.10.02 |
| 1260 DFS 와 BFS (0) | 2021.10.02 |
