[알고리즘 중급 1/3] 분할 정복 (이분 탐색 / 병합 정렬(merge sort) / 퀵 정렬(quick sort)

분할 정복

- 분할 정복은 문제를 2개 또는 4개 이상의 작은 부분 문제로 나눈 다음 (분할) 다시 합쳐 정답을 구할 수도 있음. (정복)

- 분할 정복이 dynamic programming 과 가장 다른 점은, 부분 문제가 중복되지 않는 다는 것이다. dp 에서는 부분 문제들이 중복되어 memoization 을 통해 중복을 제거했다면, 분할 정복에서는 부분 문제 끼리 중복이 없기에 부분 문제를 1번씩만 풀면 된다.

 

 

---

이분 탐색

가장 중요한 분할 정복 알고리즘이다. 리스트의 크기가 N 이라면, 정렬되어 있는 리스트에서 값을 빠르게 찾는 알고리즘

 

- 시간 복잡도 : O(lgN)

아래 배열에서 4를 찾아보자.

L = 0 M = 4 R = 8

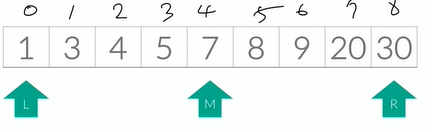
찾으려는 값(4) 와 M 중간값(7) 을 비교해보면, 찾으려는 값(4) 가 더 작기 때문에 -정렬되어 있는 리스트이기 때문에- 4는 현재의 M 보다 작은 index 에 있을 것이다. 그러므로, R 을 M - 1 로 옮긴다.

L = 0 M = 1 R = 3

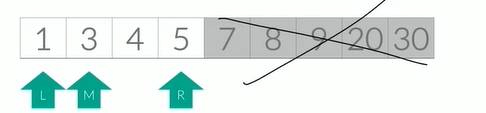
찾으려는 값(4) 와 M 중간값 (3) 을 비교해보면 찾으려는 값(4) 가 더 크기 때문에 4는 현재의 M 보다 큰 index 에 있을 것이다. 그러므로, L 을 M + 1 로 옮긴다.

L = 2 M = 2 R = 3

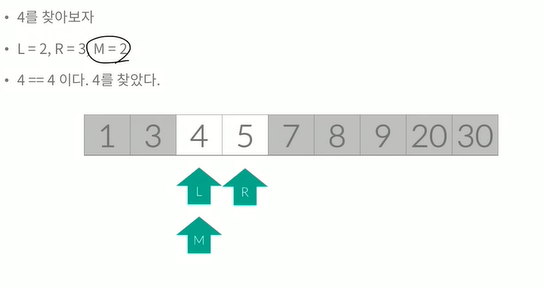
찾으려는 값 과 중간값이 같아졌다. 4를 찾았다.

 

만약, 위와 같은 배열에서 없는 값(2) 를 찾으려고 한다면, L 과 R 의 대소관계( L <= R -> L < R) 가 뒤바뀐다. 그러므로, L 과 R 의 대소관계가 뒤바뀐다면 배열에는 없는 값을 찾는 것이다.

• 숫자카드
• 숫자카드 2

 

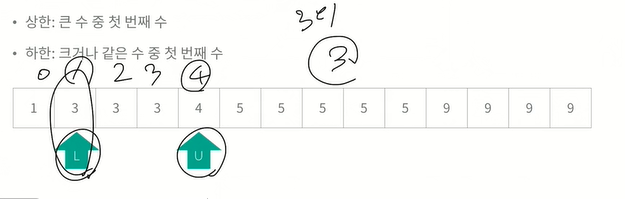
상한과 하한

상한 : 큰 수 중 첫째수

하한 : 크거나 같은 수 중 첫번 째 수

상한 - 하한 = 찾는 수의 개수

찾는 수가 없으면, 상한과 하한이 겹치게 되며, 수의 개수가 0이다.

 

 

---

머지 소트

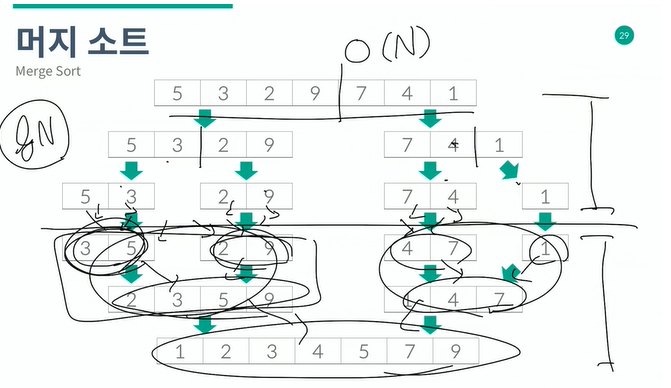
나누는 데 걸리는 시간 : lg N

합치는 데 걸리는 시간 : N

 

머지 소트에서 배열을 합치는 알고리즘을 구현해보자

• 배열 합치기 11728

a 는 원래 배열 / b 는 임시 배열 / i 는 a의 왼쪽 idx / j 는 a 의 오른쪽 idx / k 는 b의 idx

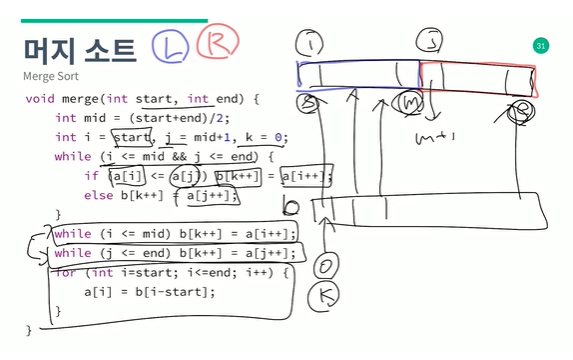
1. 왼쪽 오른쪽을 비교해가며 b에 넣는다.

2. 왼쪽 오른쪽 중 하나가 먼저 끝나면, 남은 배열을 b 에 넣는다.

3. b 를 뒤집어 a 에 넣는다.

분할은 어떻게 할까

 

 

---

퀵 소트

 

- 평균적인 상황에서 최고의 성능

https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html

- 강의에서의 퀵 소트 구현 (피벗을 중간 값으로 잡음)

#include <iostream>
#include <algorithm>
using namespace std;
// quick sort 구현

vector<int> vec{5, 1, 4, 2, 8, 2, 5, 4,6,1,9,6,9,1};

// partiton 함수 실행 이후 low ~ high 는 마지막 store index 를 기준으로 좌측은 작은 수 우측은 큰 수로 정렬됨.
// 반환하는 storeIndex 는 좌우의 대소를 나누는 기준점임.
int partition(int low, int high){
	int pivotIndex = (low + high) / 2;
	int pivotValue = vec[pivotIndex];
	
	swap(vec[pivotIndex], vec[high]); // swap
	
	// 시작점부터 끝점까지, 피봇 값보다 작으면 왼쪽으로 보내고, 크면 오른쪽으로 보냄
	int storeIndex = low;
	for(int i = low; i < high; i++){
		if(vec[i] < pivotValue){
			swap(vec[i], vec[storeIndex]);
			storeIndex++;
		}
	}
	swap(vec[storeIndex], vec[high]); // 재 swap
	return storeIndex;
}

void quicksort(int low, int high){
	if (low < high){
		int pivot = partition(low, high);
		// 나눈 것을 기준으로 좌측을 재정렬
		quicksort(low, pivot - 1);
		// 나눈 것을 기준으로 우측을 재정렬
		quicksort(pivot + 1, high);
	}
}


int main(){
	for(int i : vec){
		printf("%d ", i);
	}
	cout << endl;
	quicksort(0, vec.size() - 1);

	for(int i : vec){
		printf("%d ", i);
	}
	cout << endl;

}