문제 해설 및 주의사항
1. 프리오더 / 인오더 / 포스트 오더?
- 트리를 탐색하는 방법이다.
a. 프리오더 : 루트 -> left -> right 순으로 탐색
b. 인오더 : left -> 루트 -> right 순으로 탐색
c. 포스트 오더 : left -> right -> 루트 순으로 탐색한다.
풀이
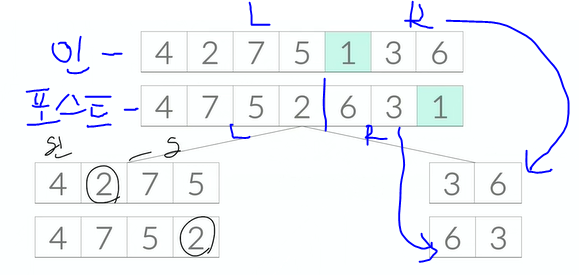
1. 포스트 오더를 먼저 보자.
- 포스트 오더는 마지막에 루트를 방문하므로, 포스트 오더의 마지막 순회 지점이 루트라는 것을 알 수 있다.
2. 인오더를 보자.
- 인오더는 left 전부를 탐색하고, 루트를 탐색하고, right 전부를 탐색하는 것이다.
그러므로, 포스트 오더에서 루트 정보를 얻은 것을 바탕으로 트리의 왼쪽과 오른쪽을 나눌 수 있다.
포스트오더에서 루트 값을 1이라고 알고, 인오더 한 것이 4 2 7 5 1 3 6 이라면, 1을 기준으로 left tree 와 right tree를 구분케할 수 있다.
3. 시간 복잡도는?
- 포스트 오더에서 루트를 찾는데 O(1)
- 인오더에서 루트 인덱스를 찾는데 O(N)
- 인오더에서 분할 하여 계속 루트 인덱스를 찾는데 O(N)
이므로, O(N^2) N 의 최대치가 100,000 이므로 불가능하다.
이때, 시간을 줄이는 방법을 도입해야 하는데, 인오더에서 루트 인덱스를 찾는 시간을 O(1) 로 만드는 방법이 있다.
바로, 인오더에서 각 정점이 어디에 있는지를 배열에 미리 저장해두는 것이다.
position[i] : i 번 정점이 인오더에서 몇 번째에 위치하는지를 저장한다.
풀이코드
#include <iostream>
using namespace std;
const int MAX = 100000;
int n;
int inorder[MAX];
int postorder[MAX];
// position[i] : i 번 정점이 인오더에서 몇 번째에 위치하는지를 저장한다.
int position[MAX + 1];
void solve(int in_start, int in_end, int post_start, int post_end){
// 시작과 끝의 대소가 둘 중 하나라도 바뀌면 끝
if(in_start > in_end || post_start > post_end) return;
// 포스트오더에서 루트를 가져온다.
int root = postorder[post_end];
// 프리오더로 출력해야 하므로 root 를 바로 출력
printf("%d ", root);
// root 가 인오더에서 몇 번째에 위치하는지를 p에 저장한다.
int p = position[root];
// 왼쪽 자식의 수
int left = p - in_start;
// 왼쪽 자식 호출
solve(in_start, p - 1, post_start, post_start + left - 1);
// 오른쪽 자식 호출
solve(p + 1, in_end, post_start + left, post_end - 1);
}
int main(){
scanf("%d", &n);
for(int i = 0; i < n; i++) scanf("%d", &inorder[i]);
for(int i = 0; i < n; i++) scanf("%d", &postorder[i]);
for(int i = 0; i < n; i++){
position[inorder[i]] = i;
}
solve(0, n - 1, 0, n - 1);
cout << endl;
}
아쉬웠던 부분 / 오답 원인 / 개선해야 할 점
1. 항상 핵심 로직을 명확하게 정리해두고 시작해야한다.
'ps > 분할 정복' 카테고리의 다른 글
| [분할 정복] 사분면 1891 (0) | 2021.10.21 |
|---|---|
| [분할 정복] Z 1074 ○ (0) | 2021.10.16 |
| 하노이탑 이동 순서 (boj.kr/11729) (0) | 2021.10.14 |
| 종이의 개수 (boj.kr/1780) (0) | 2021.10.14 |
