문제 해설 및 주의사항
맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다. 최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.
만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.
N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)
풀이
1. 최단 경로이다. 시간 복잡도는?
- 풀이 중 문제가 두 가지로 나뉜다.
a. 각각의 벽을 빈 칸으로 바꾼다. (모두 바꿔보는데 NM)
b. 그 위치에서 이동할 수 있는 칸의 개수를 구한다. (각 칸의 개수를 구하는데 NM)
총 O( (NM)^2) 이 걸린다. N 과 M 의 최대가 1,000 이므로 1억을 훌쩍 넘는다. 불가능하다.
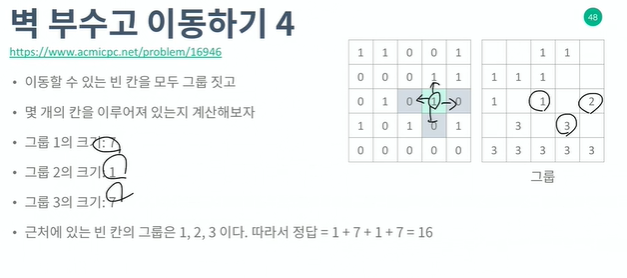
2. 시간을 어떻게 줄일 수 있을까?
풀이코드
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <set>
#include <tuple>
using namespace std;
const int MAX = 1000;
int n, m;
// 칸
int a[MAX][MAX];
// 방문했는지 안했는지 (false 가 초기상태)
bool check[MAX][MAX];
// 해당 칸이 무슨 그룹인지 (-1 이 초기상태)
int group[MAX][MAX];
// 그룹의 크기가 몇인지
vector<int> group_size;
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
void bfs(int sx, int sy){
int g = group_size.size();
// bfs 시작 처리
queue<pair<int, int>> q;
q.push(make_pair(sx, sy));
check[sx][sy] = true;
group[sx][sy] = g;
int cnt = 1;
while(!q.empty()){
int x, y;
tie(x, y) = q.front(); q.pop();
for(int k = 0; k < 4; k++){
int nx = x + dx[k];
int ny = y + dy[k];
// 범위 체크
if(nx >= 0 && nx < n && ny >= 0 && ny < m){
// 방문하지 않았고, 빈 칸이라면
if(!check[nx][ny] && a[nx][ny] == 0){
check[nx][ny] = true;
group[nx][ny] = g;
q.push(make_pair(nx, ny));
cnt++;
}
}
}
}
group_size.push_back(cnt);
}
int main(){
cin >> n >> m;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
scanf("%1d", &a[i][j]);
}
}
fill_n(&check[0][0], MAX*MAX, false);
fill_n(&group[0][0], MAX*MAX, -1);
// 모든 칸을 순회하면서, bfs 를 실시한다. 이때, 모든 칸에 그룹을 지어준다.
for(int i = 0 ; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i][j] == 0 && check[i][j] == false){
bfs(i, j);
}
}
}
// 모든 칸을 순회하면서, 벽인 칸을 찾아내어, 주변 칸들의 그룹을 찾고, 그 그룹들의 사이즈의 합을 출력한다.
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
// 벽이라면
if(a[i][j] == 1){
set<int> near;
for(int k = 0; k < 4; k++){
int nx = i + dx[k];
int ny = j + dy[k];
// 범위 체크
if(nx >= 0 && nx < n && ny >= 0 && ny < m){
// 다음 칸이 빈 칸이라면
if(a[nx][ny] == 0){
// 주변 칸의 그룹을 push
near.insert(group[nx][ny]);
}
}
}
int ans = 1;
for(int index : near){
ans += group_size[index];
}
cout << ans % 10;
}
// 벽이 아니라면
else{
cout << 0;
}
}
cout << '\n';
}
}
퇴고
- 시간을 줄이기 위해서 사용한 방법, 모든 빈 칸들을 연결 요소의 집합으로 분류하여, 벽과 연결되어 있는 집합들의 크기만 더하는 방법이 인상깊었다. 그 와중 사용된 것이 set STL 인데, 중복된 집합이 주변에 있을 수 있기에 사용하였다.

반응형
'ps > bfs & dfs' 카테고리의 다른 글
| [dfs/ bfs] [정점의 재정의] 돌 그룹 (0) | 2021.10.24 |
|---|---|
| 타겟 넘버 (0) | 2021.10.23 |
| [정점의 분리] [최단 거리] 벽 부수어 이동하기 2206 (재) (0) | 2021.10.23 |
| [bfs] [연결 요소] 바이러스 14502 (재) (0) | 2021.10.23 |
| [bfs][최단거리][역추적] DSLR 9019 ○ (0) | 2021.10.23 |
